First we decide upon two hyperparameters; $N$ and $L$. $N$ is the maximum number of points that can be present in a voxel and $L$ is minimum voxel size to be followed even if there are more than $N$ points in a voxel.
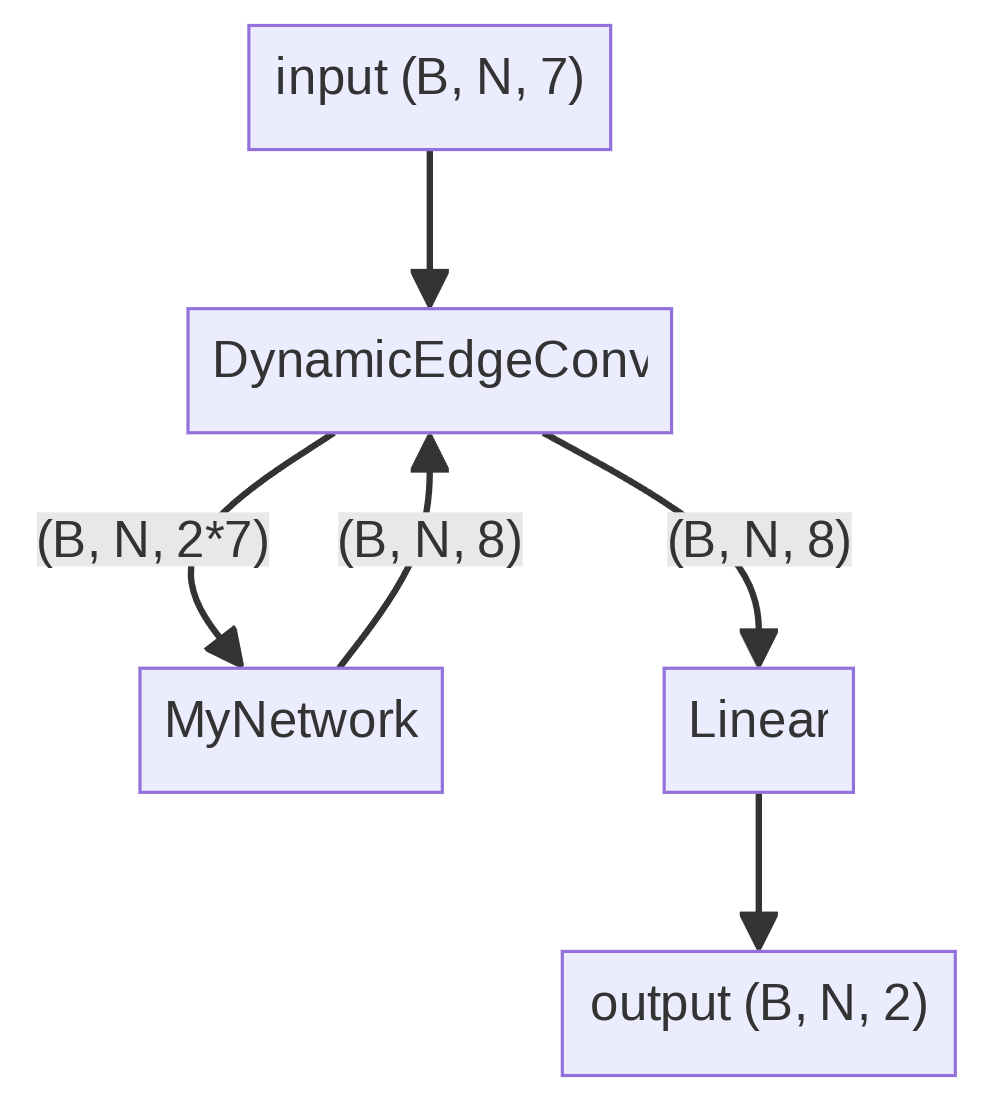 
center the image and preserve aspect ratio